| y = 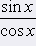 Function cotangens is given by equation y = 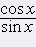
|
D(f) of function tangens is set of those real numbers x, for which is true 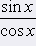 . Taht is when cos x ¹ 0. In interval <0, 2p) is value of function cosinus = 0 for . Taht is when cos x ¹ 0. In interval <0, 2p) is value of function cosinus = 0 for 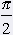 and and 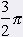 . . |
D(f) of function y = tg x set of every real nu,ber different from od 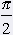 + 2kp and + 2kp and 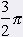 + 2kp, where k Î Z. + 2kp, where k Î Z. |
Else said, D(f) of function y = tg x is set of every x Î R, for which x ¹ (2k + 1)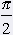 , while k Î Z. , while k Î Z.
|
D(f) fo function cotangens is set of those every real numbers x, for which is true 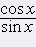 . Thats when sin x ¹ 0. In interval <0, 2p) is value of function sinus =0 for 0 and p. It means that D(f) of function y = cotg x is set of every x Î R, pre ktoré sa x ¹ kp, while k is individual whole number èíslo. . Thats when sin x ¹ 0. In interval <0, 2p) is value of function sinus =0 for 0 and p. It means that D(f) of function y = cotg x is set of every x Î R, pre ktoré sa x ¹ kp, while k is individual whole number èíslo.
|
|
Veta:
Let k be individual whole number. For every real number x, x ¹ (2k + 1) 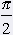 , is: , is:tg(-x) = -tg x, and for every real number x, x ¹ kp, is: cotg(-x) = -cotg x. |
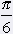 = 30° = 30° |
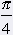 = 45° = 45° |
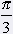 = 60° = 60° |
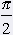 = 90° = 90° |
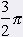 = 270° = 270° | |||
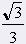 |
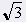 |
||||||
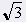 |
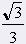 |
|
Functions tangens and kotangens are uneven. We know that functions y = sin x, y = cos x are periodic with period 2p. It means that also functions y = tg x a y = cotg x are periodic and one from their period is 2p. For every x from D(f) of function y = tg x is: 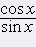 where k Î Z. |
| Similar end is by function cotangens. When studying tangens and cotangens it is enough to study on interval <0, 2p). |
Function y = tg x is set of every couples [x, ym], where x ¹ (2k + 1)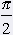 . Fuction y = cotg x is set of every couples [x, yn], where x ¹ kp. . Fuction y = cotg x is set of every couples [x, yn], where x ¹ kp. |
|
Veta : Let k be individual whole number. For every x ¹ (2k + 1) 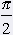 is: is:tg (x + kp) = tg x and for every x ¹ kp is: cotg(x + kp) = cotg x | ||
|
Because smalest period of function tangens is p, its enough to study part of function on which D(f) is opened interval of length p. Similar by function cotangens.
Lets study for example functions
k1: y = tg x, x Î (-p/2, p/2)
k2: y = cotg x, x Î (0, p) Functions k1 a k2 have these propeties: Arent limited No maximum no minimum Value field is in both cases set of every real numbers. Function k1 is increasing on whole interval (-p/2, p/2) Function k2 decreasing on interval (0, p) Folowing tables shows where are definition values of functions k1 a k2 positive or negative èísla. |
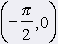 |
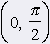 | |
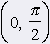 |
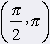 | |
| Additional tasks |