Law of cosine

In arbitrary triangle ABC is:

a2 = b2 + c2 - 2 b c cos a

b2 = a2 + c2 - 2 a c cos b

c2 = a2 + b2 - 2 a b cos g

Mathematical evidence :

At first we'll apply this demonstration on triangles with no quadrants. By using following sketches we'll get:

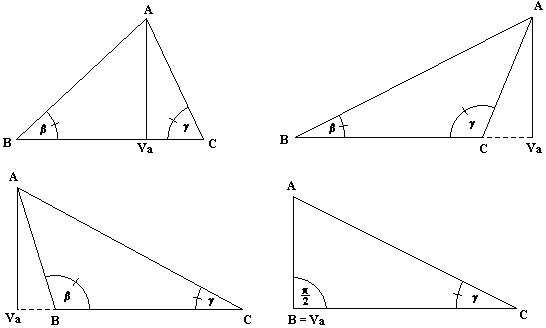
a = |BVa| + |VaC| = c cos b + b cos g ,              a = |BVa| - |CVa| = c cos b - b cos ( p - g ) = c cos b + b cos g ,              a = |VaC| - |VaB| = b cos g - c cos ( p - b ) = c cos b + b cos g .        We have used here this equation cos (p - j) = - cos j. We'll get the same result in all three cases: a = c cos b + b cos g, which is also true (as we can see it from fourth sketch) when one of the angles b, g in triangle is quadrant. After raise to the 2nd power we'll get:              a2 = ( b cos g + c cos b )2 ,              a2 = b2 cos2 g + c2 cos2 b + 2 b c cos b cos g ,              a2 = b2 ( 1 - sin2 g ) + c2 ( 1 - sin2 b ) + 2 b c cos b cos g ,              a2 = b2 + c2 - b2 sin2 g - c2 sin2 b + 2 b c cos b cos g .        We can rewrite one expression of law of sine as: b sin g - c sin b = 0. After its raise to the 2nd power we'll get:              b2 sin2 g + c2 sin2 b - 2 b c cos b cos g = 0 , this allows to continue in previous calculating like this:              a2 = b2 + c2 + 2 b c ( cos b cos g - sin b sin g ) ,              a2 = b2 + c2 + 2 b c cos ( b + g ) ,              a2 = b2 + c2 + 2 b c cos ( p + a ) ,              a2 = b2 + c2 + 2 b c cos a . With that is 1st equation prooved. The other two can be prooved analogicaly.

---

---