In impedance triangle ABC, in which quadrant is angle g, is:
c2 = a2 + b2
2nd power of length of hypotenuse in impedance triangle is equal to sum of 2nd power of lengths of its rest sides.
As evidence of Pythagoras' theorem is enough to use equation: c2 = a2 + b2 - 2 a b cos g from Law of cosine and substitute g = p / 2 .
Evidence of inverted Pythagoras' theorem:
We'll make evidence by dissension: Let's predict that c2 = a2 + b2, while angle opossite to side c isn't quadrant. We can construct triangle ABC1 so that:
|AC1| = |AC|,
|angle AC1B| = 90o
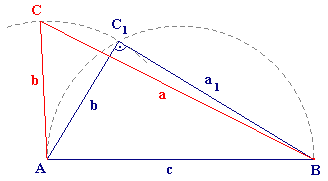
a12 + b2 = a2 + b2
We'll substract b2 : a12 = a2
a1 and a are positive then we have: a1 = a - triangles ABC and ABC1 are identical by sss (side, side, side) but aren't identical in matching included angles ACB and AC1 - dissension. Assumption that angle ACB is quadrant is wrong. That means that if c2 = a2 + b2 is true then this triangle is impedance with quadrant opposite to side c - QED.
Evidence by similarity :
We'll use Euklides' theorem:
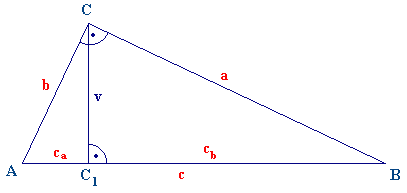
a2 + b2 = c.ca + c.cb = c ( ca + cb ) = c2 - > c2 = a2 + b2.
